


We have attempted to write most of these web pages in such a way as to be understood
by any visitor. This site is however designed primarily as a reference for
professional astronomers who are directly involved in this field of research. Some
sections therefore necessarily become very technical. We do hope however that non-astronomers
will visit and we would like them to actually profit from reading our pages.
We have therefore attempted to provide here a brief description of most of the basic
concepts behind the survey, such that anyone with a good understanding of physics
will understand.

Under certain conditions, like those in the nucleus of a QSO,
all atoms can be made to emit light at particular wavelengths. The precise wavelengths,
or colours, at which each atom radiates are unique, which effectively gives each
type of atom a sort of `finger-print'. Hydrogen, for example has a series of
emission lines seen at 6562.8Å,
4861.3Å, 4340Å, 4102.8Å,
4102.8Å, 3888.7Å,
3834.7Å and 3798.6Å. This is only a representative sample. There are many more
lines. If we see features in an object's spectrum at precisely these wavelengths, we know that
Hydrogen must be present in that object.

Light is an electro-magnetic wave, just like the signal emitted by police radar
speed cameras. We can measure the
speed with which a QSO is moving away from us in almost the same way as a
radar gun measures the speed at which you are approaching it. Light, sound or indeed
any wave is perceived differently when it comes from a moving source. If that
source is approaching the observer, the wave is squashed up onto itself making
the wavelength shorter. For light, this makes it bluer. For sound (e.g., an
approaching fire engine siren) it makes the sound higher pitched. For a receeding
source, light gets redder and sounds get deeper. We measure the apparent speed of
a QSO by looking at features in the spectrum which we know are leaving the QSO at
a particular wavelength (i.e., colour), but by the time we observe them are observed
to be much redder. This is redshift. We define the redshift z scale such that the
observed wavelength is 1+z times the emitted wavelength.
For example, let us consider the H beta line.
This is the one mentioned above at 4861·3Å. If we observe that line to actually be
at 9722·6Å, then we say that the object has a redshift of z=1, because
9722·6=2 × 4861·3.
There is of course a difference between the speed camera and our measurements though. In a speed camera, a beam is sent out from the gun to bounce off the approaching vehicle. The radar source and observer are both stationary (they are both the same thing!), but the signal has been bounced off a moving target. We clearly cannot do this with QSOs. They are far too remote, but since they emit their own light we do not need to. If cars glowed like QSOs, the police could do the same and would not need radar guns!
The plot below puts all this together and demonstrates how QSOs look different when they are at different redshifts.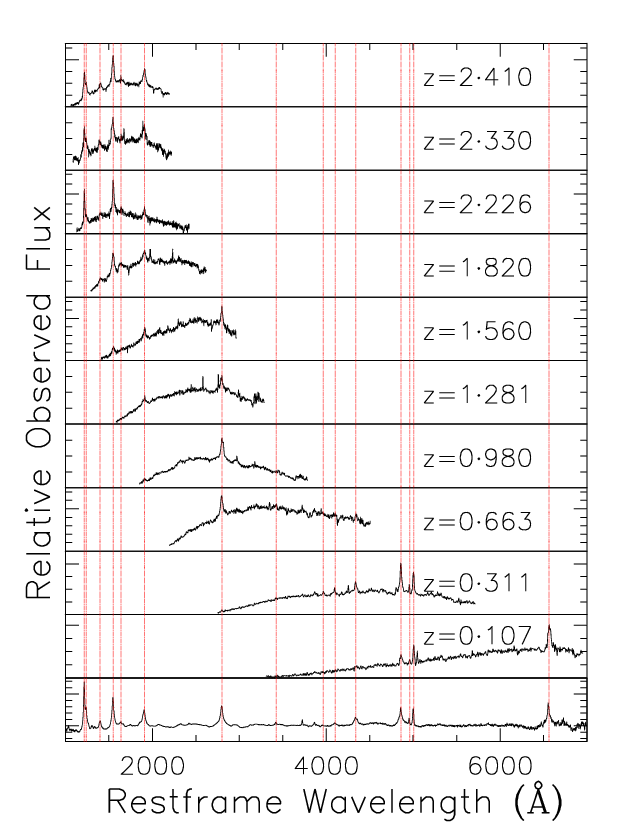
This plot shows ten QSOs at various redshifts each projected back to its rest wavelength to show it how it was when emitted from the QSO rather than how it was observed when it reached the telescope. For comparison there is a composite spectrum at the bottom. The composite was created by adding together 10000 spectra, thereby creating one mean spectrum which covers the full wavelength range. You can see how the section of the QSO spectrum which we observe changes with redshift. For very low redshift QSOs, we can actually observe the visible wavelengths. For very distant objects though the ultra-violet part of the spectrum has been redshifted into the visible and is what we observe. The light which was in the visible range when it was emitted, has now been redshifted far out into infrared where we cannot observe it.
After we have observed an object, we determine its redshift simply by comparing it to the composite at the bottom to see how we can best line up all the features to match. We then see how far we had to slide the observed spectrum along the scale to make it match and that is the objects redshift.
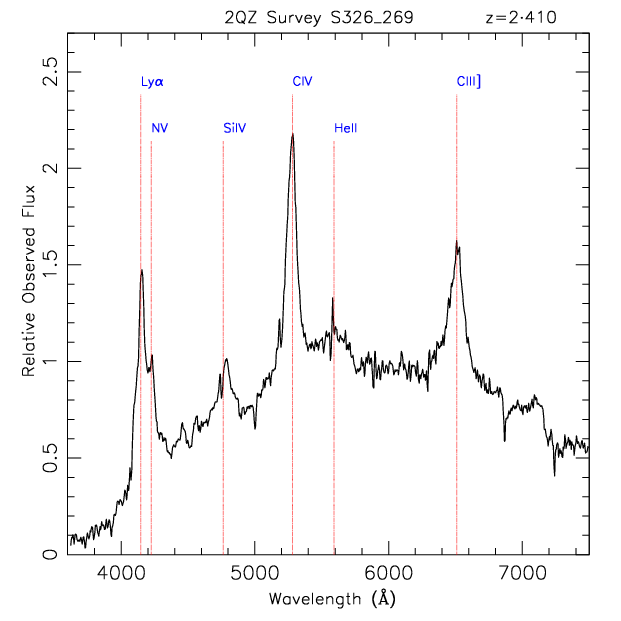
For comparison, we plot below the observed spectrum for the highest redshift object above. You can see that the shape of the spectrum is the same. It is simply observed with longer wavelengths. In this plot, we also label the lines to show which atoms are responsible for each one. The atoms shown here are Hydrogen (Ly), Nitrogen (N), Silicon (Si), Carbon (C) and Helium (He). The roman numerals signify the physical state of the atom at the time the light was emitted. For example, this spectrum contains lines from both CIV and CIII, two different states of carbon. If you are interested, all ten spectra are shown in their observed wavelengths here.
Å : Angstrom : A unit of length which strictly is not part of standard, internationally recognised SI units. It is however very popular among astronomers. 1 Å = 10-10 m = 0·0000001 mm. Visible light has wavelengths in the range 4000(blue) - 7000(red) Å. The spectra from 2dF cover a slightly wider range of wavelegth; 3500 - 8000 Å. (This, incidently and irrelevently, is rather similar to the range visible to a goldfish.)
| The 2QZ team (Thu Aug 9 15:54:27 BST 2001 by RJS) |

This site is kindly hosted by Astrophysics Research Institute of Liverpool JMU |